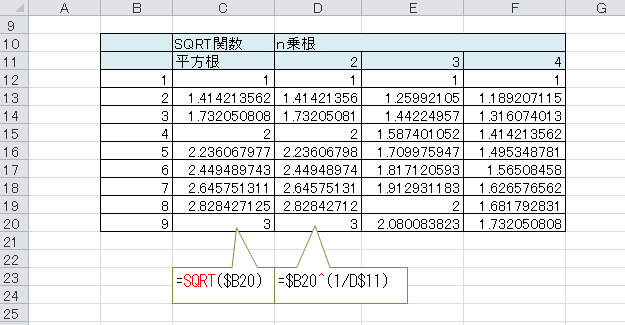
小数部の数値のみを抽出したい場合があります。
一般的には、INT関数を使用して、元の数値から整数部を引くことで求められますが、
MOD関数を利用しても求めることができます。
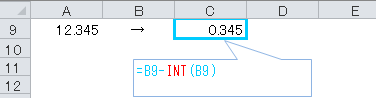
INT関数を使って整数部を引く方式
上記のような短い式の場合は問題ありませんが、下記のような場合には不便です。
下記は、指定された変数の小数部を求めまています。
下記のように、変数を検索して、小数部を求めると
式全体が長くなります。
また、
同じ計算(VLOOKUP)を2度行なっているのが気に入りません。
このような場合、作業セルに、VLOOKUP(C15,E15:F19,2,FALSE)の部分を一旦計算しておくのが一般的でしょうが、
作業セルを使いたくない場合は困ります。
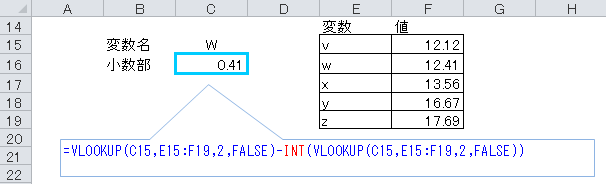
余りを求める−MOD関数
このような場合、
余りを算出する関数
MODを使用して、1度の計算で小数部を取り出す方法があります。
この場合、除数には「1」を指定します。
1で割った余りといのは少し奇妙ですが、ちゃんと機能します。
(余りは整数とは限らないのですね!)
スッキリした式になりました!
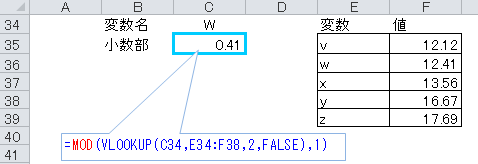
999という数字を考えてみます。
これの10を底とする対数(常用対数)を計算すると、2.999565488・・・
つまり、 2<LOG
10999<3
10の指数をとると、10
2<999<10
3
すなわち、10
2は2+1桁なので、999は3桁となります。
一般的な記述では、Xの桁数は、
INT(LOG10X)+1
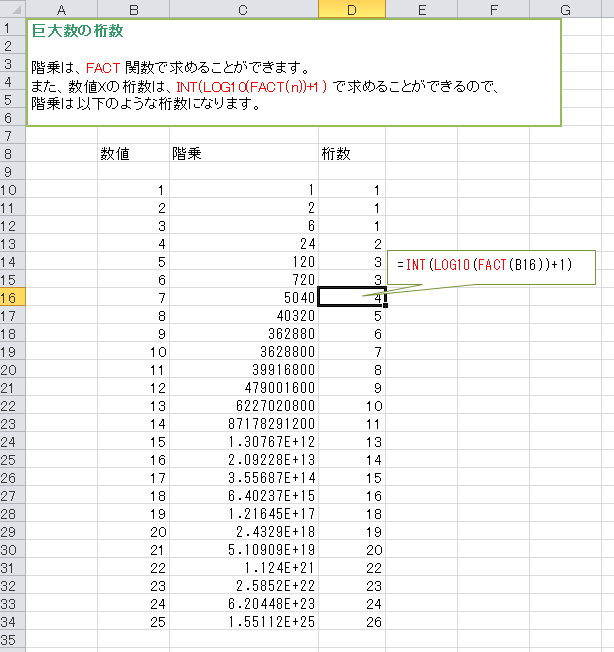
以下は、エクセルで階乗の桁数を計算したもの。
階乗:
FACT関数
階乗の計算は、1からnまでの順列組合せなどに登場!
(最初の選び方はn通り、次はn−1、その次はn−2通り・・・・・、よって、n×(n−1)×(n−2)・・・・1)
すなわち、上の表から、3x3のマス目に1〜9の数字を重複することなく並べる順列組合せ数は9の階乗となり、6桁の数となることが分かります。
4x4では16の階乗で14桁(10兆の位)、5x5では25の階乗で26桁(
十穣の位)となります。おそろしや〜