再度、新しいファイルをダウンロードしてください。
勤務は文字としては計算が面倒なので、数値に置き換えます。
0:休み 1:日勤 2:早出 3:遅出 など
単一勤務
ここでは分かり易くするために、勤務は1種類(出勤するか、しないか)から始めます。
目標値
・日々の要員数が必要人数と一致
最初から完全一致とすると難しいかもしれないので、ここでは、
要員数と必要人数の差の絶対値合計の最小値とします。セルK11
最初から完全一致とすると難しいかもしれないので、ここでは、
要員数と必要人数の差の絶対値合計の最小値とします。セルK11
変化するセル
・セルC4:I8 - 1:割り当てる 0:割り当てない
制約条件
・変化するセルの値は、0か1
→ 値は1以下の非負整数

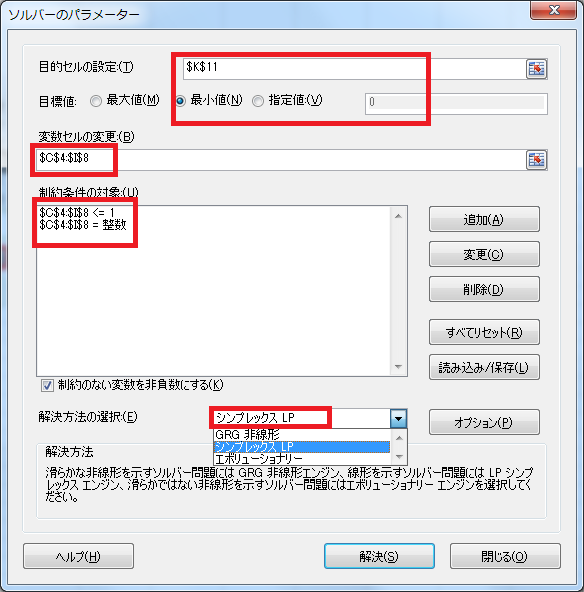
解は、ほとんど瞬間的に求まります。
→ 値は1以下の非負整数
ここで使用されている式は、足し算と絶対値を求める関数ABSのみ。
線形問題として簡単に処理できますので、「解決方法の選択」は「シンプレックス LP」


解は、ほとんど瞬間的に求まります。