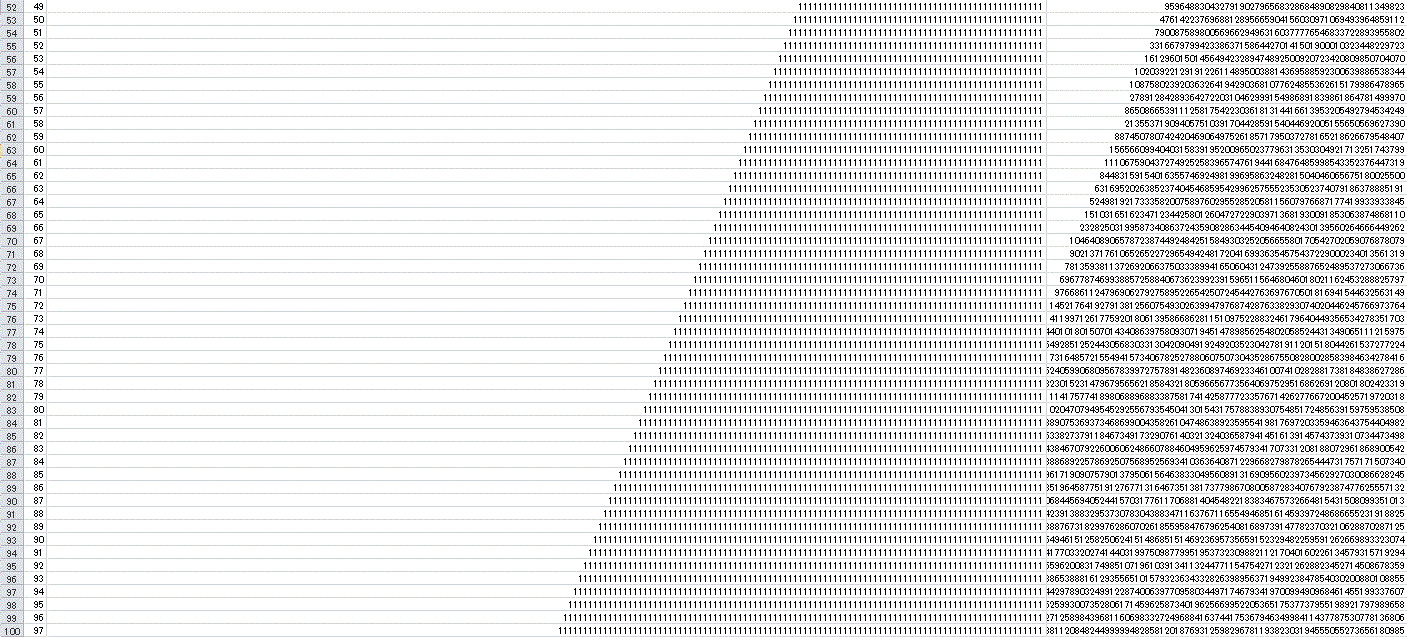素数判定テスト

フェルマーの小定理の対偶を用いて確率的に素数を判定する方法です。

　　フェルマーの小定理

p が奇素数であるとき、p と互いに素な整数 a において

a^ｐ−１ ≡１  (mod ｐ)

　　が成立。

また、　a^ｐ−１ ≡１  (mod ｐ)　が成り立つとき、p は、かなりの確率で素数と言えます。

フェルマーテストにおいて、素数ではないのに確率的素数であると判定される数を 擬素数 と呼びます。
擬素数かどうかは底により決まり、ある底で擬素数であっても他の底で擬素数であるとは限りません。
そのため、複数の底でテストを行うことで、信頼性を高めることができきます。

しかしながら、それでも、それ自身と互いに素である全ての底においてフェルマーテストを通過してしまう擬素数が存在し、それらはカーマイケ ル数と呼ばれています。
小さい順に、561, 1105, 1729, 2465, 2821, 6601, 8911, …
と、無数に存在することが判明しています。

なお、この定理の対偶をとると、自然数 n が合成数であるための十分条件を与えます。
　　（　対偶：命題「AならばB」の対偶は「BでないならAでない」　）


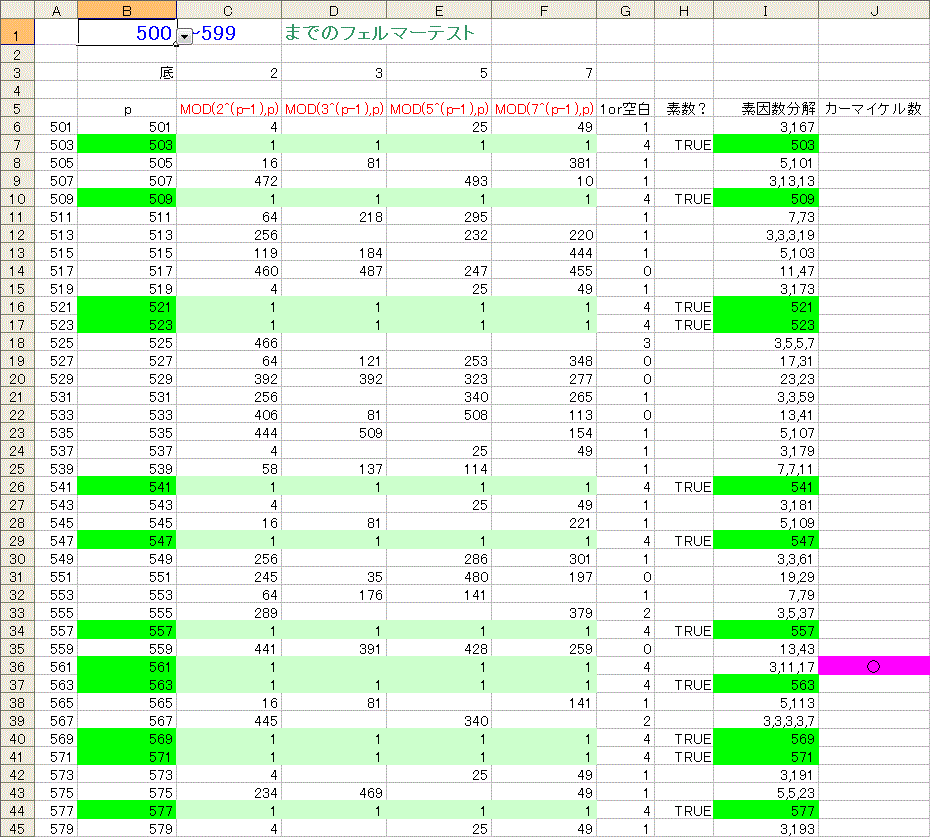
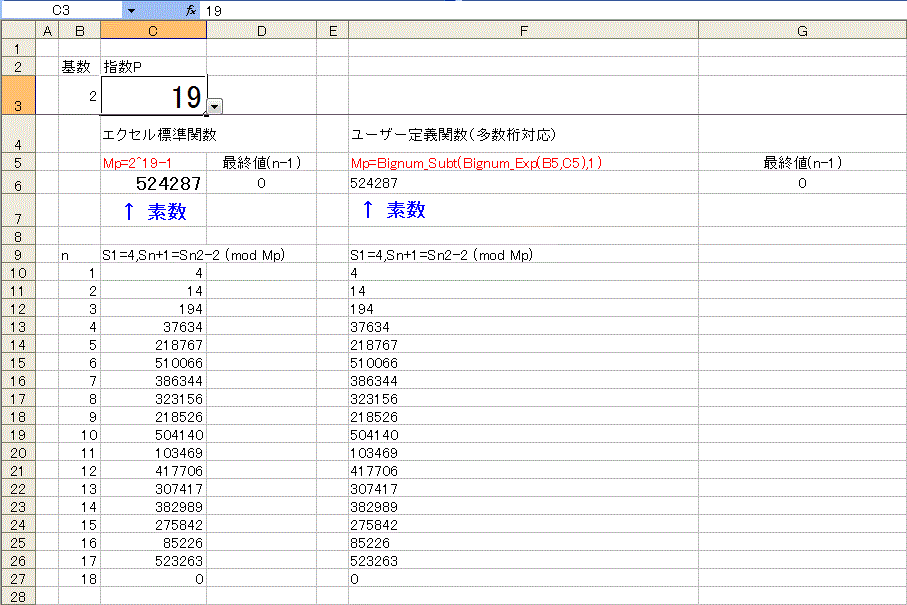
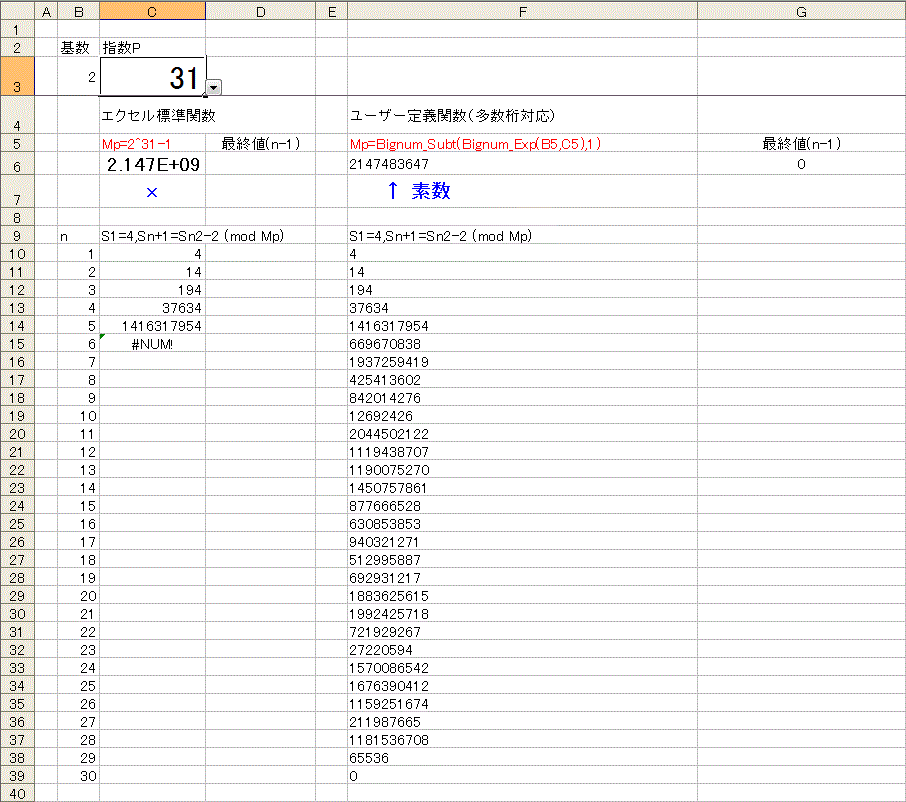
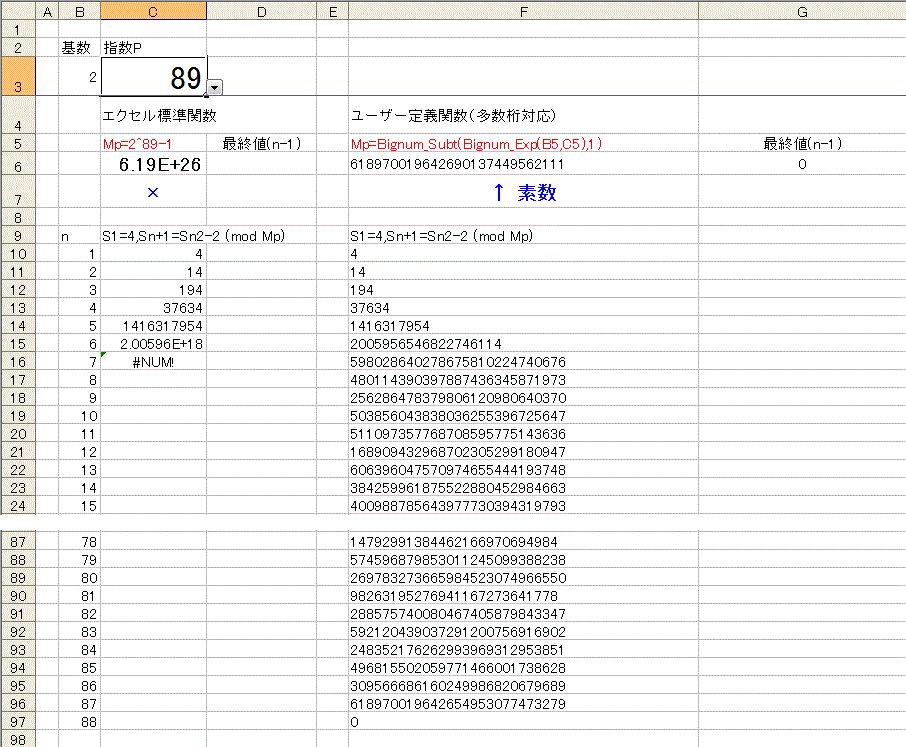
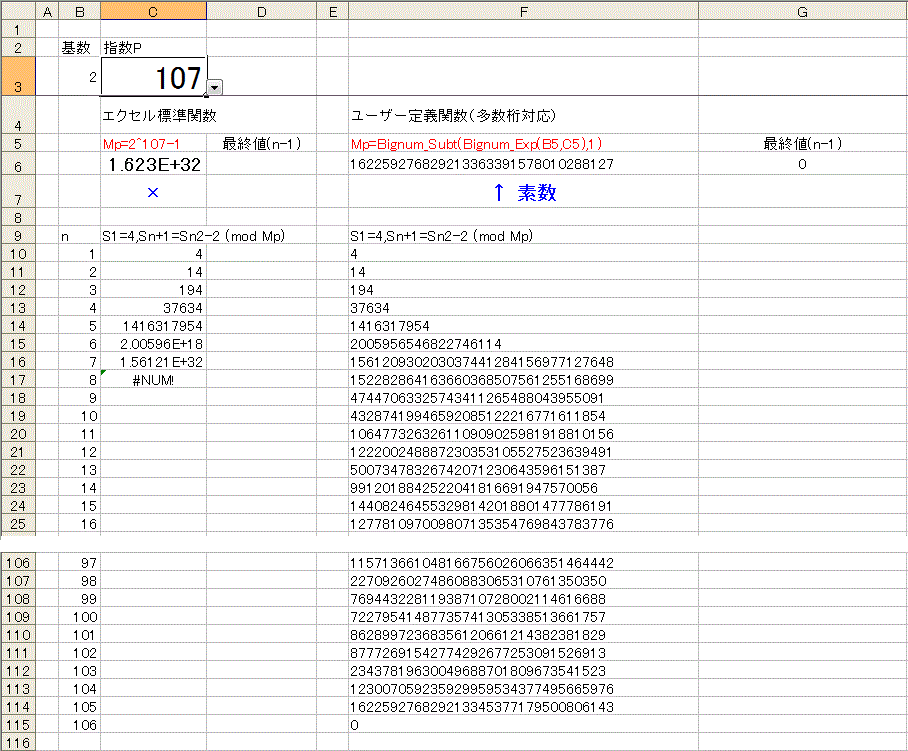
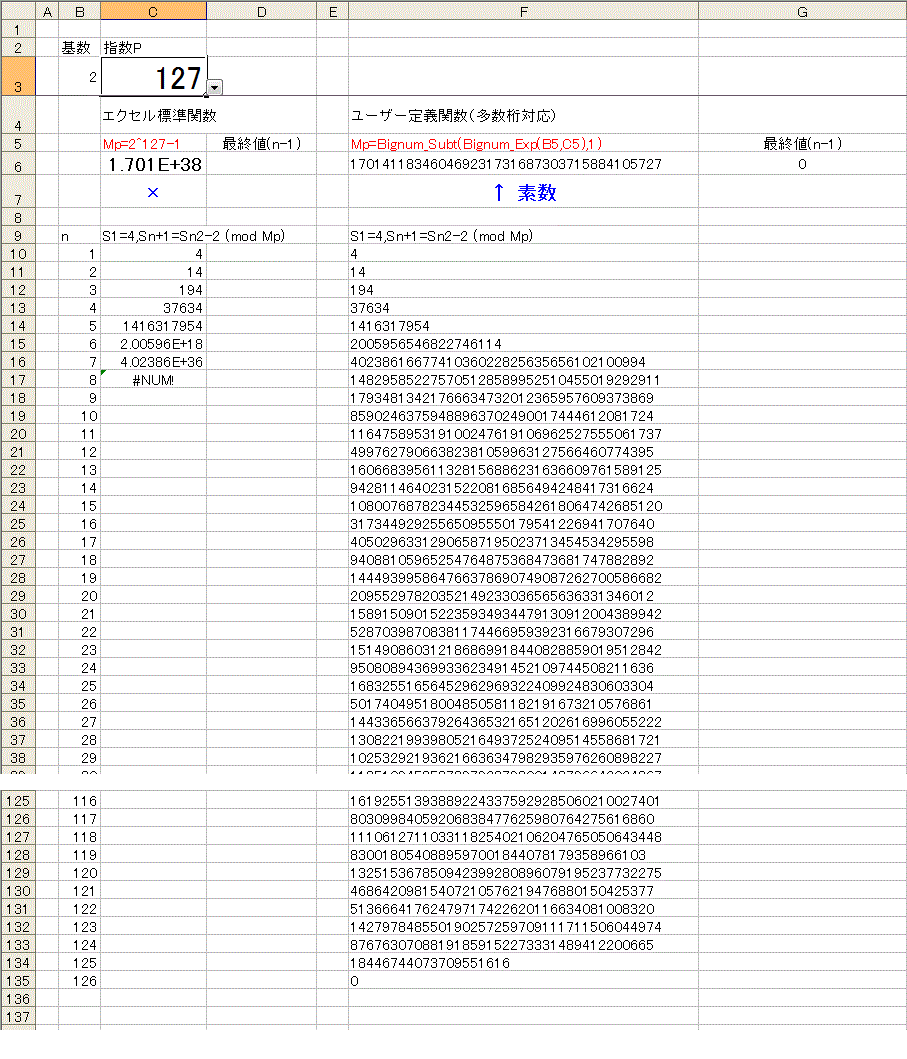
下図は、p が５０１〜５９９の数値で試したもの。
セルB1に数値を入力（または選択）すると９９個分（偶数は省略）の数値を判定します。

５６１に底が２、３，５，７の場合をパスする合成数が現れています。

レプユニット素数とは、「全て同じ数値が並んだ素数」のことです。

とは言っても、偶数だと２で割り切れるので、奇数でないといけません。
かといって、７７７７７７７　は、そもそも７で割り切れるので、
レプユニット素数の候補は、
１１１１・・・・１１１１
のように、１が並んだ形式しか有り得ないことになります。

実際試してみます。

判定には、前項の「フェルマー・テスト」を使用。

A列が桁数。B列に桁数に応じた１の連続を作成
E列でフェルマーの小定理に対応した「べき剰余」を求めます。

以下が結果。色付き部分が素数候補。







１９５桁までに、２桁、１９桁、２３桁の３つしかありませんでした。

次に登場するのは、３１７、１０３１　とのこと。

１０３１桁には手が出せませんが、３１７桁は計算可能なので、フェルマー・テストで試して見ます。
所要時間　約２０分　( 3.30GHz,4.00GB )

確かに、１になりました。フェルマーテストは使えそうです。

試し割りやエラトステネスの篩のような総当りを除いて、一般の数値が素数であるかを判定する方法はありません。
しかし、特殊な形式の数値の場合は、素数であるかを判定する方法があります。

そのひとつがメ ルセンヌ数と呼ばれる数値のグループです。

　メルセンヌ数　(Mersenne number）

　　　2の冪よりも 1 小さい自然数、すなわち 2ⁿ − 1（n は自然数）の形の自然数
　　　2進数で表記すると、n 桁の 11…11 である。


　メルセンヌ素数　(Mersenne prime)

メルセンヌ数のうち素数となる数値群

1644年にマ ラン・メルセンヌは、 2ⁿ − 1 が素数になるのは、n ≤ 257 では、n = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257 だけであると主張した。しかしその主張の一部は誤っていて、リストに含まれていない M₆₁, M₈₉, M₁₀₇ も素数であり、リストに含まれている M₆₇, M₂₅₇ は合成数であることが後に判明した。

現在判明している素数になるメルセンヌ数は、小さい方から
 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521,607 ・・・・

メルセンヌ数は、リュカ・テストと呼ばれる方法で素数であるかを判定でき、現在、最大素数の発見レースは、このメルセンヌ数にて行われ ています。

最新のメルセンヌ素数は
48番目　2013年1月25日に発見　n= 57,885,161　桁数は17,425,170

　リュカ・テスト( Lucas Test )　　

メ ルセンヌ数:　Mp=2^p-1 [pは素数]　 において

　　数列S_n
　　　　S₁=4
　　　　S_n+1=S_n²-2　(mod Mp)　　(n≧1)

　  Mpが素数であれば、　S_p-1=0 (mod Mp)　となる。

以下、3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127　にてテストしたもの。

Ｃ３にて指数の値を選択、または入力すると数列が計算され、数列の最後が「０」であれば”↑ 素数”と表示されます。

Ｃ列はエクセルの標準数を使用して計算したもの。
ｎ＝３１で桁あふれになります。

Ｆ列は巨大桁整数演算の項で作成したユーザー定義関数を使用して計算したもの。
かなりの桁数まで計算できますが、ｎが１２７で１，２分の時間がかかりますので、
それ以上の桁を試す場合は覚悟を決めてから実行して下さい。

　　セルF10の数式：　=4
　　セルF11の数式：　=IF(OR(B11="",F10="0"),"",Bignum_Div_Remainder(Bignum_Subt(Bignum_Exp(F10,2),2),$F$6))

「素数であることが確率的に十分高い」なんて、数学的に意味があるの？


複数の素数判定法を組み合わせて、素数である可能性が極めて高い場合、

実用的な暗号作成（RSA暗号な ど）に使用できます。

これを用いて、正確な素数を生成するより、確率的な素数生成（または判定）は、極めて高速、かつ簡単に生成できます。


数学的には無意味でも、工業的な用途には十分な例の一つです。



とりあえず、以上