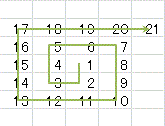素数あれこれ
ここでは、素数に関する関する簡単なプログラムを作成。
素数の一覧、素数の判定、最大公約数/最小公倍数、そして、
不思議な図形、「
ラウムの螺旋」を描画します。
ダウンロードするサンプルファイルはExcel2003形式で作成しています。
行列数の制限(65,536行、256列)がありますので、大きな広範な出力値を使用する場合は、
Excel
2007-2013形式の「
マクロ有効ブック」に変換して下さい。
・素数(prime number)とは?
素数とは、「1とその数自身以外に正の約数がない、1 より大きな自然数のこと。」のことです。
1は素数でない?
1が素数であるとしても、大部分の数学の命題はそのまま有効ですが、素因数分解の一意性は成り立たなくなります。
例えば 15 の素因数分解は、1が素数であると仮定すると、 15 = 3 × 5 = 1 × 3 × 5
の2通りの素因数分解が可能となり、「一意性」が成り立たなくなります。
これを避けるために、1は素数から除外されています。)
素数は奇数?
偶数である「2」は素数なので、奇数とは限りません。
しかし、2より大きい整数では成り立ちます。
「-3」は素数?
定義から、素数は自然数なので、負の数は素数ではありません。
素数は無限に存在
ユークリッド(エウクレイデス)『原論』(紀元前3世紀頃)第9巻命題20にて、素数は無数に存在することが示されています。
以下、その証明
n個の素数を小さい順にp1、p2、p3・・・pn をとる。
q=p1×p2×p3・・・×pn を考えると、qはある素数(少なくとも自分自身)で割り切れるが、p1、p2、・・、pnでは割り切れない。
すなわち、p1、p、・・、pn以外の素数が存在することを意味する。
任意の素数のリストから、リストに含まれない新たな素数が得られるので、素数は無数に存在する。
この証明は、よく誤解されることがあります。
これは、新しい素数を具体的に与えるものではありません。
また、素数を小さい順に掛けて1を加えても素数になるとは限りません。
実際、 2 × 3 × 5 × 7 × 11 × 13 + 1 = 59 × 509 となり、合成数となります。
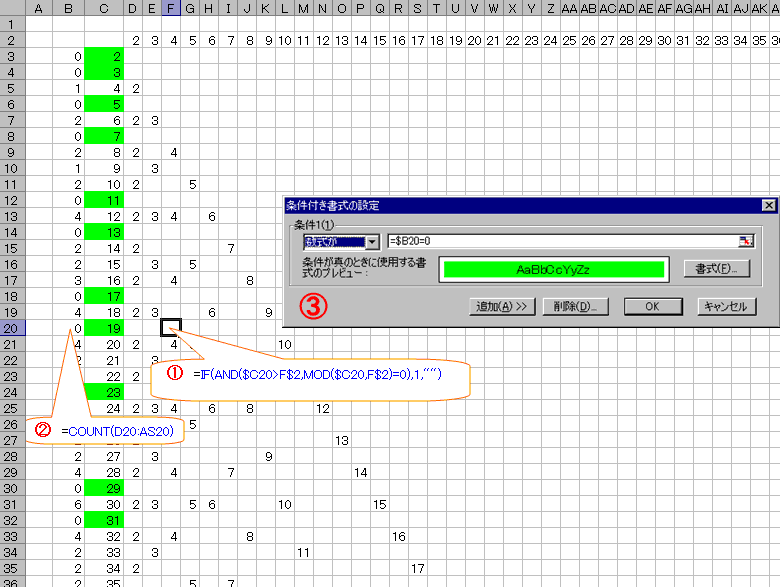
素数一覧表を作成
・数式で作成
ここで言う数式とは、素数の数列を表す数式ではなく、数式で合成数(割り切れる)かを判定して、
自分より小さい全ての数で割り切れるかを調べる数式である。
一つでも割り切れたら素数でない。
以下、数式の手順
行見出し、列見出しに、2以上の連続する数値を作成しておく
①:C列の数値を対象として、2行目の数値で割ってみる。
(ただし、C列の数値より小さい数値に限る)
C列の数値より小さく、割り切れたらその数値を表示。以外は空白
②:B列に①で計算した数値の個数を表示する(空白はカウントされない)
③:条件付書式で、B列の値(割り切れた数値の個数)が0の場合、緑色に塗る。
この
色付けされた数値が
素数と
なる。
また、表示されている数値の列が
約数である。
VBAで作成
上記の方法では、どんなに頑張っても255以下の数値(EXCEL2010では65,535)までの素数しか求められない。
数値列を奇数だけにすれば倍になるが、たいした違いは無い(それより、2の扱いに困ってしまう!)
そこで、VBAの出番!
該当の数値より小さい整数(1を除く)で順に割っていき、すべての整数で割り切れなかったら、その数値は素数。
が、そのままでは、計算に多数重複するので、
ここでは、なるべく、計算回数を少なくなる方法として「
エラトステネスの篩(ふ
るい)」を使用することにする。
エラトステネス(Eratostenes)の篩
ギリシャの哲学者・エラトステネスが考案したとされるアルゴリズムで、目標以下の素数一覧を効率よく作成する。
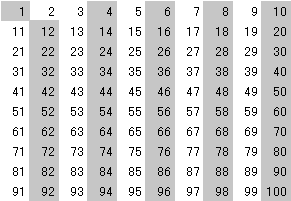
1.目標とする整数の一覧を作成
2.整数一覧から2より大きい2の倍数を除去
3.一覧に残っている次の整数(この場合3)の倍数(2倍以上)を除去
4.同様に、一覧に残っている次に大きい整数(5,7,11・・)の倍数を除去
5.上記を目標値の平方根(以下の最大整数)まで繰り返す
平方根を超える合成数(素数の積で表せる)は存在しない。
最終的に整数一覧に残ったものが素数の一覧となる。
| 2の倍数を除去 |
3の倍数を除去 |
 |
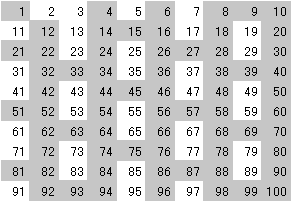 |
| 5の倍数を除去 |
7の倍数を除去 |
 |
 |
使用したVBAコード
Private Sub cmdEratosthes_Click()
'
' エラトステネスの篩(ふるい)
'
'-------------------------------
' 前処理
'-------------------------------
cmdCancel.Enabled = True
Application.Calculation = xlCalculationManual '自動計算オフ
'シート初期化
Columns("C:C").Select
Range(Selection, Selection.End(xlToRight)).Clear '値クリア
Range("Count") = ""
Range("Ratio") = ""
Range("Time") = ""
Range("Cal_Count").Select
Dim w() As Integer '作業用配列
Dim Nmax As Long '調査する値の最大値
Nmax = Val(Range("Cal_Count")) '検査する数値の最大値
RowCount = Val(Range("RowCount")) '1列の表示行数
'-----------------------------------
' 入力チェック
'-----------------------------------
If Cells.Rows.Count < Nmax Then
MsgBox "行数がオーバーします!"
GoTo MyEnd
ElseIf Cells.Columns.Count < GetCol(Nmax, RowCount, COl_ST) Then
MsgBox "列数がオーバーします!"
GoTo MyEnd
End If
'-----------------------------------
ReDim w(Nmax) '作業域確保
Dim i As Long, k As Long
Dim t As Long '計測タイマ
t = GetTickCount
'-------------------------------
' 素数生成開始
'-------------------------------
blCancel = False
Dim Count As Long
w(1) = 1
Count = 0 '素数個数カウンタ
For i = 2 To Nmax
If blCancel Then Exit For 'キャンセル
If w(i) = 0 Then
Count = Count + 1 '素数個数アップ
For k = 2 To Int(Nmax / i) '倍数にチェック
w(i * k) = 1 '非素数:1
Next k
Dim R As Long, C As Long 'シート上の行列番号
R = GetRow(Count, RowCount, COl_ST) '行番号取得
C = GetCol(Count, RowCount, COl_ST) '列番号取得
Cells(R, C) = i '素数を表示
End If
If (i Mod RowCount) = 0 Or i = Nmax Then
Range("Progress") = i '進捗
DoEvents
End If
Next i
MyEnd:
'-------------------------------
' 後処理
'-------------------------------
Range("Count") = Count '素数個数
Range("Ratio") = Count / Nmax '比率
Range("Time") = (GetTickCount - t) / 1000 '所要時間
Application.Calculation = xlCalculationAutomatic '自動計算オン
cmdCancel.Enabled = False
End Sub
'------------------------------------------------------------------
' 内部関数
'------------------------------------------------------------------
Private Function GetRow(n As Long, RowCount As Long, COl_ST As Long)
'
' 番号からシート内の行番号生成
'
GetRow = ((n - 1) Mod RowCount) + 1 '行番号
End Function
Private Function GetCol(n As Long, RowCount As Long, COl_ST As Long)
'
' 番号からシート内の列番号生成
'
GetCol = Int((n - 1) / RowCount) + COl_ST '列番号
End Function
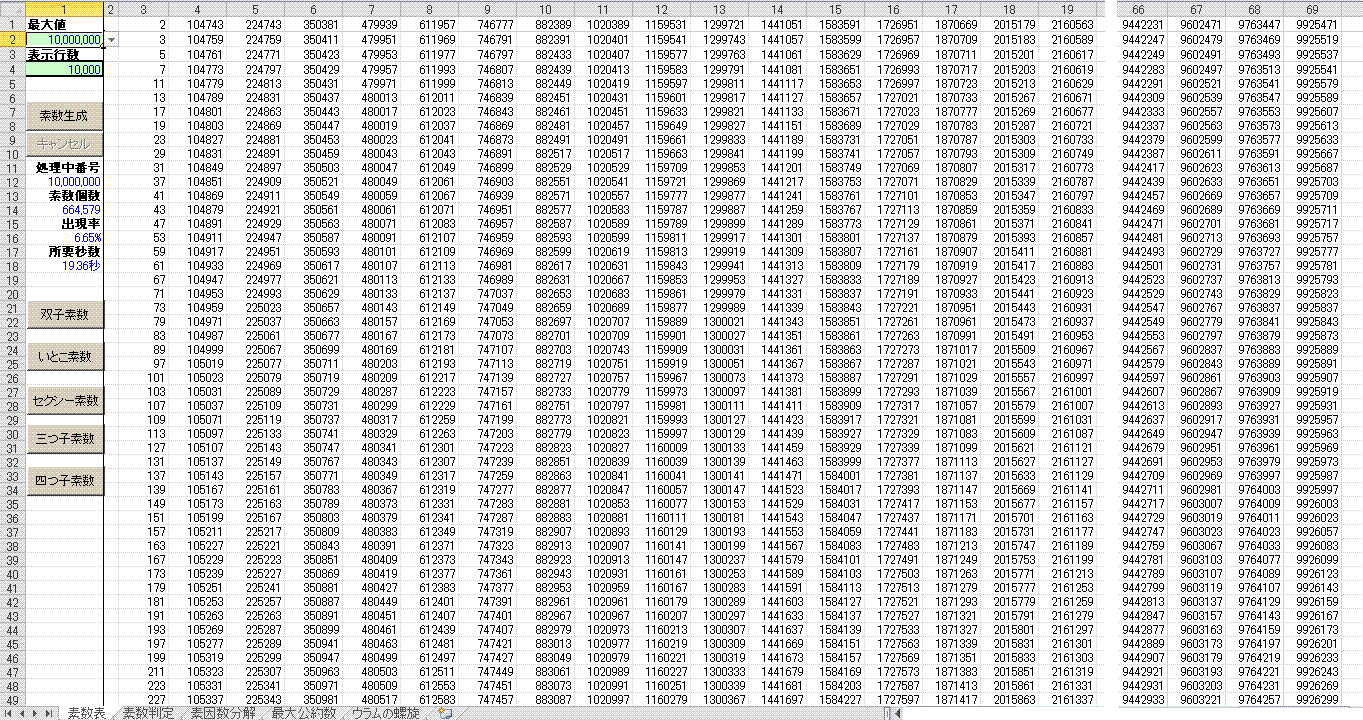
素数一覧表
数は1000万以下の整数から素数一覧を作成したもの
テキストファイル形 式 (1列1万行)
・素数個数: 664、579個
・出現率: 6.65%
・所要時間 19.36秒
プロセッサ: Intel(R) Pentium(R) CPU G630 @ 2.70GHz 2.70
GHz
実装メモリ(RAM): 2.0GB
システムの種類: 64ビットオペレーティングシステム
双子素数
双子素数(twin prime)とは、差が 2 である2つの素数の 組。
2 と 3 の組を除くと、双子素数はもっとも数の近い素数の組である。
双子素数の例としては、 3 と 5 、 11 と 13 、 857 と 859 などがある。
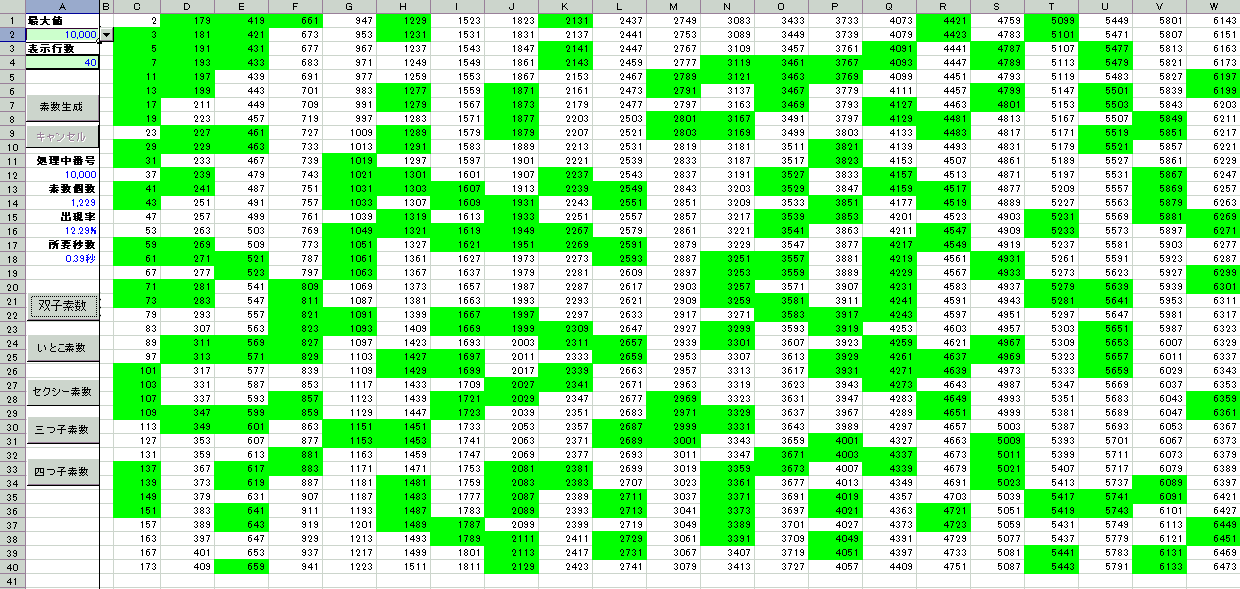
いとこ素数(cousin primes)
差が4である素数の組
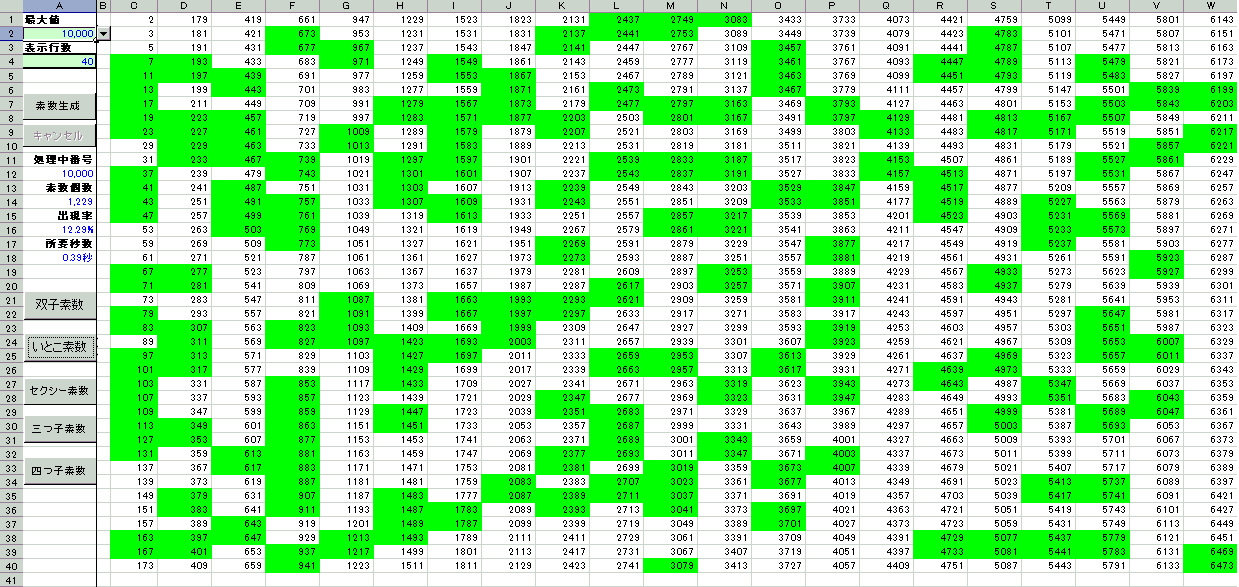
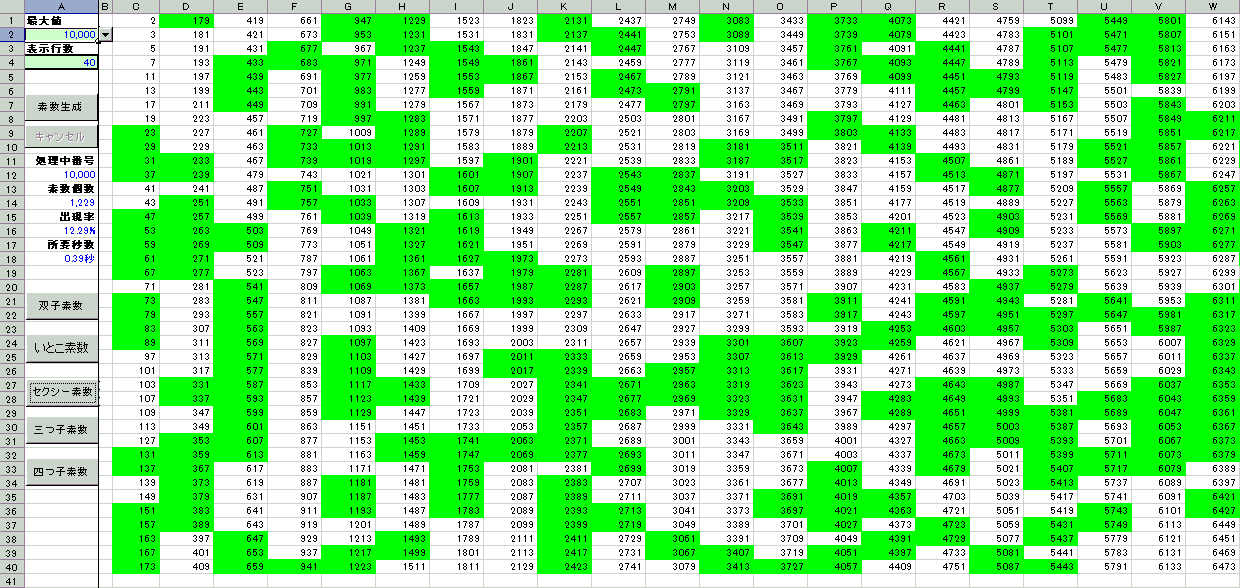
セクシー素数(sexy primes)
差が 6 の素数の組 (
p,
p + 6) である。
・・セクシーとは「色っぽい」という意味ではなく、ラテン語で 6 が sex であることに由来する。
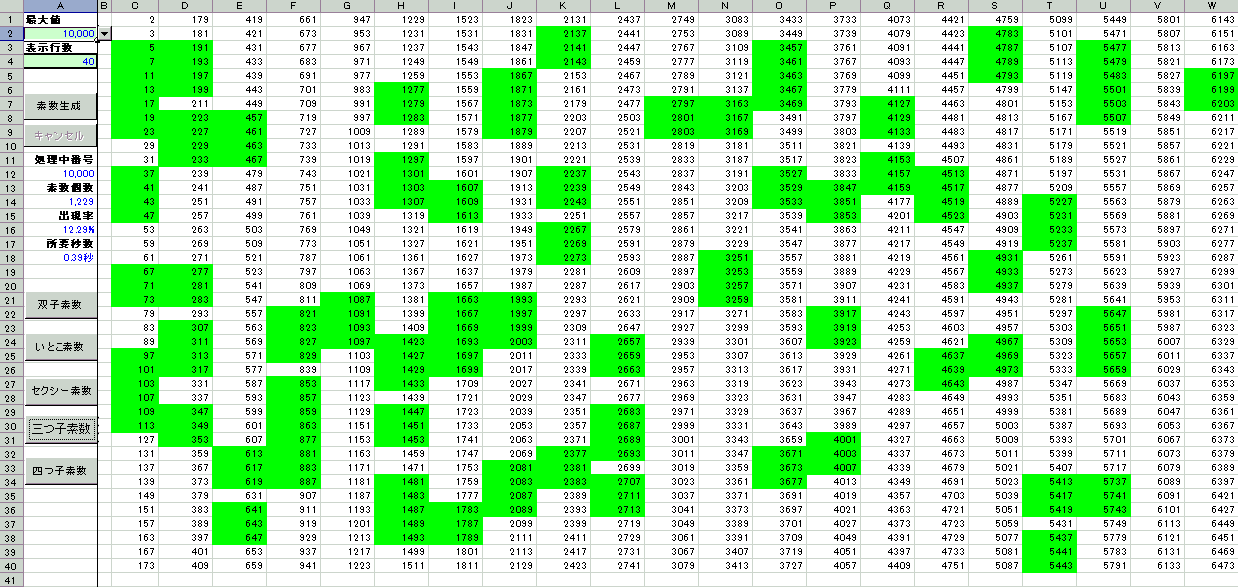
三つ子素数(prime triplet)
(
p,
p + 2,
p
+ 6) または (
p,
p + 4,
p + 6) の形をした、素数の 三つ組と定義す
る。
「(
p,
p + 2,
p + 4)
の形をした素数の三つ組」と定義しないのは、その中に必ず 3 の倍数を含むことになり、
このような定義にすると (3, 5, 7) しか存在しないことになるからである。
よって、多少、人為的な定義なので、あまり数学的には意味がないかもしれない。
「素数生成」後に「双子素数」ボタンをクリックすると、色付けされる。
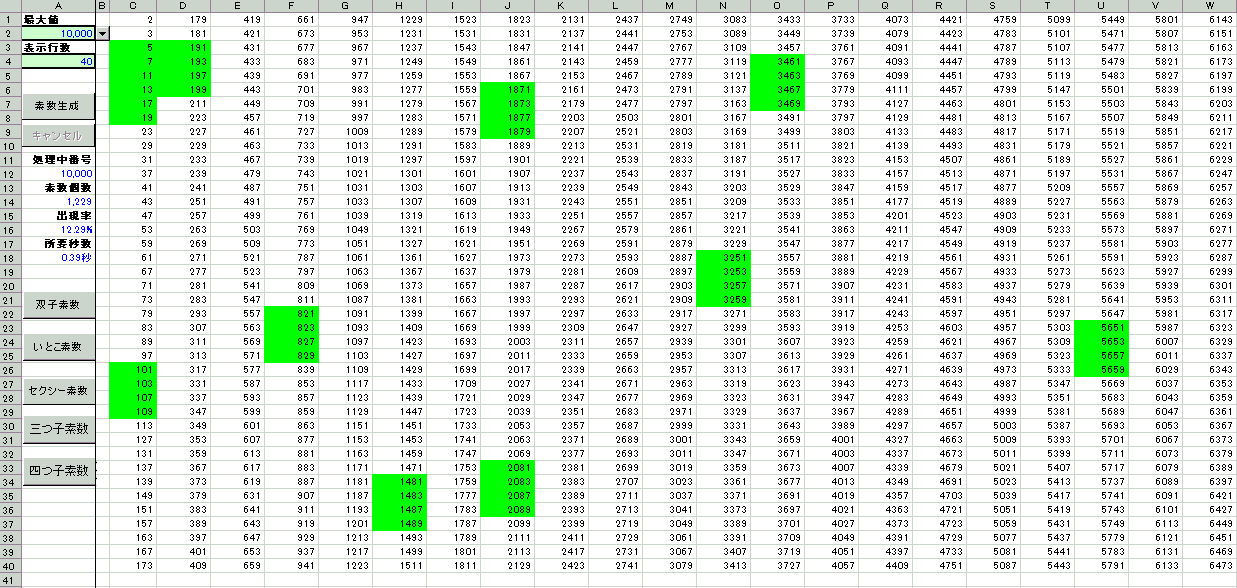
四つ子素数(prime quadruplet)
p, p+2, p+6, p+8 がすべて素数であるような数の組をいう。
ここで p と p+2 の組および p+6 と p+8 の組はいずれも
双
子素数であり、 p+2 と p+6 の組は
い
とこ素数であり、 p と p+6 の組および p+2 と p+8 の組はいずれも
セ
クシー素数であり、 p と p+2 と p+6 の組および p+2 と p+6 と p+8 の組はいずれも
三
つ子素数である。
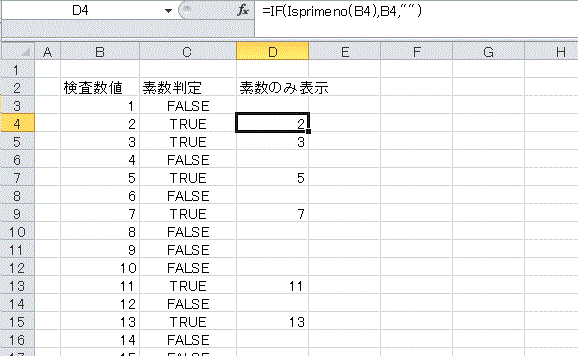
素数判定
ユーザー定義関数を作成し、与えられた数値が素数であるかを簡単に判定します。
TRUEが返れば素数、FALSEが返れば合成数。
処理自体は説明の必要がないほど簡素。
与えられた数値を2以上、平方根以下の整数で片っ端から割ってみます。
割り切れたらFALSEを返す(1は無条件にFALSEとする)
使用したVBAコード
Function IsPrimeNo(数値) As Boolean
'
' 素数判定
'
' 方式 :試し割り 3~SQR(Num)
'
' 戻り値:TRUE:素数 FALSE:合成数
'
Dim i As Long
Select Case 数値
Case 1: IsPrimeNo = False '1は素数でない
Case 2: IsPrimeNo = True '2は素数
Case Else
If (数値 Mod 2) = 0 Then '2で割り切れたら素数でない
IsPrimeNo = False
Else
IsPrimeNo = True
For i = 3 To Int(Sqr(数値)) Step 2 '3以上の奇数で割ってみる
If (数値 Mod i) = 0 Then '割り切れるか・
IsPrimeNo = False
Exit For '素数では無い!
End If
Next i
End If
End Select
End Function
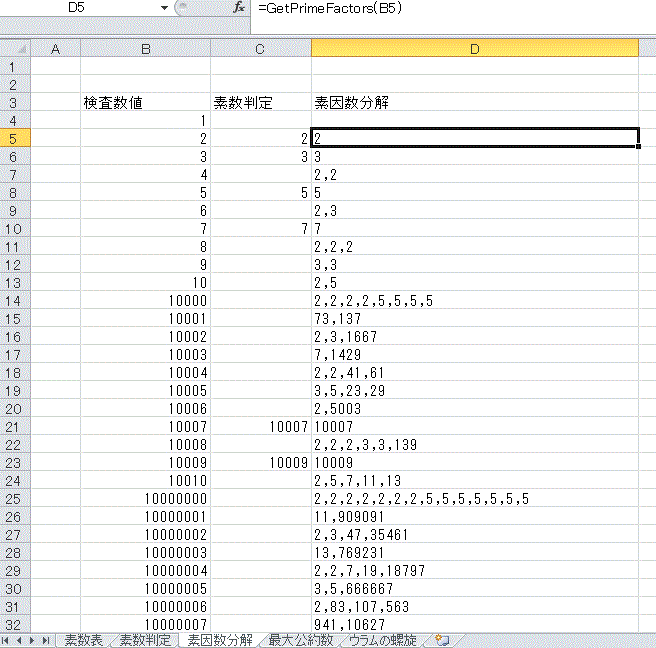
与えられた数値を素因数に分解し、カンマ区切りとして返却。
数値が素数であれば、そのまま数値を返す。
使用したVBAコード
Function GetPrimeFactors(数値)
'
' 素因数分解:Fatorization
'
Dim i As Long
Dim n As Long
Dim lngQ As Long '商
Dim lngR As Long '余り
Dim strRc '返却値
On Error GoTo MyErr
strRc = ""
n = 数値 '検査する値
i = 2 '初期因数
Do
If (n Mod i) = 0 Then
strRc = strRc & "," & i
n = n \ i
i = 2
Else
i = i + 1
End If
Loop While (i <= Int(Sqr(n))) And (n <> 1)
If n <> 1 Then strRc = strRc & "," & n '割れ残り
If Left(strRc, 1) = "," Then strRc = Right(strRc, Len(strRc) - 1) '先頭のカンマを除去
GoTo MyEnd
MyErr:
strRc = CVErr(xlErrValue)
MyEnd:
On Error GoTo 0
GetPrimeFactors = strRc '戻り値
End Function
ウラムの螺旋
素数は一見すると、ランダムに出現するように見えますが、ある規則で配置していくと、不思議な模様が浮かび上がります。
以下は、「
ラウムの螺旋」と呼ばれるもので、ポーランド出身アメリカで活躍した数学者スタニスワフ・マルチン・ウラム
(Stanisław Marcin Ulam, 1909年4月3日 - 1984年
5月13日)が退屈な会議中にメモ用紙にいたずら書きをしていて発見したそうです。
1から始まる整数を順に記入していきます。
ここでは、まず右方向に進むとし、右隣が空白であれば右方向転換し数値を記入。
この動作を繰り返すと時計方向周りの渦巻が出来ます。(図1)
次に、素数だけに色を付けます(図2)
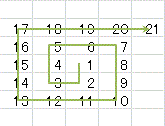 |
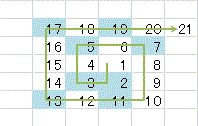 |
図1
|
図2 素数に色を付ける
|
以上の操作をエクセルのシート上で実行していくと下記のような模様が出来ます。
ここでは、まだ特徴あるパターンは見えませんが、もっと数を多くしていくと・・・・
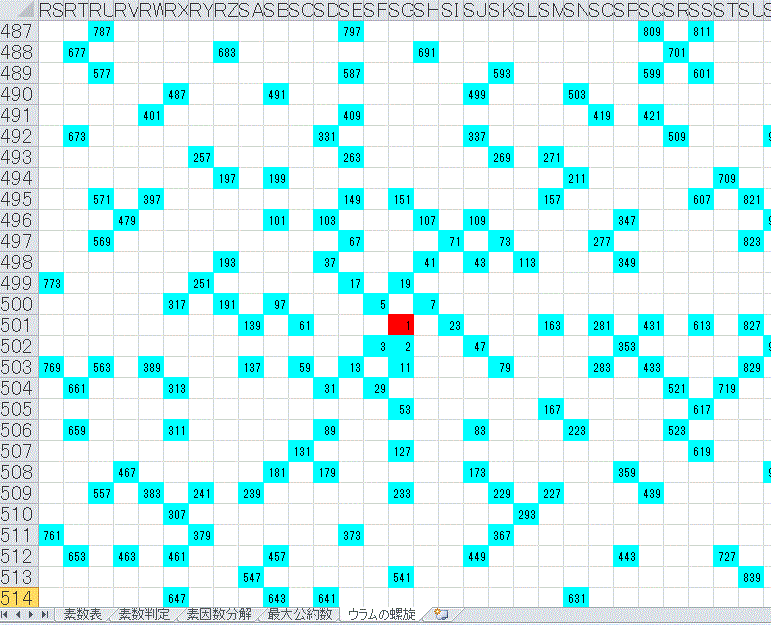
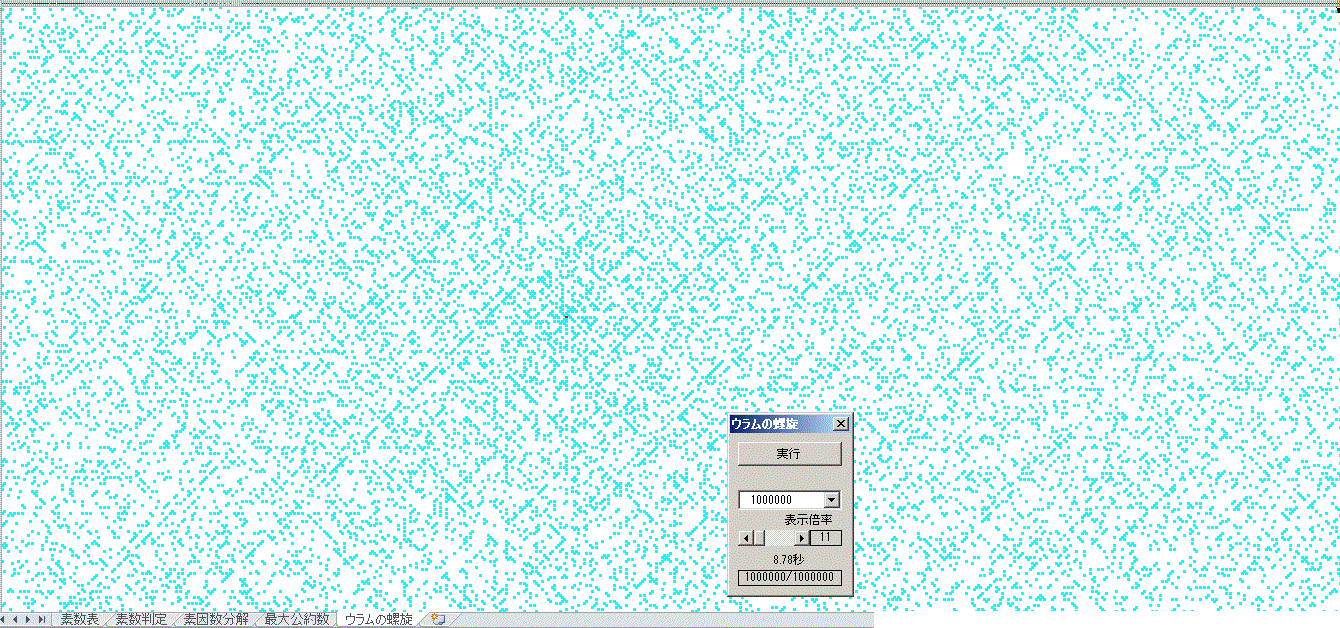
下図は100万以下の素数を描画
(ここでは
EXCEL2010を使用-EXCEL2003は255列までな
ので描画不足)
何やら、うっすらと
斜め線が見えます。
とても、偶然とは思えません。
何らかの規則が存在していることを示唆しています。
現在でも詳しいことは分かっていないとのこと・・・・
もっともっと数値を大きくしていくと、神様の姿が浮かび上がる・・・などと考えさせる不思議な模様です。
プログラム自体は簡素
使用したVBAコード
Public Sub Go(Nmax As Long)
'
' ウラム螺旋作成開始
'
blCancel = False 'キャンセルフラグ初期化
'有効列数チェック
Dim ColCnt As Long
ColCnt = Int((Cells.Columns.Count - 1) / 2) * 2 + 1 '直近奇数
If Nmax > ColCnt ^ 2 Then
MsgBox "列数をオーバーします。" & vbCrLf & vbCrLf & _
Format(ColCnt ^ 2, "###,##0") & "以下にして下さい。"
Exit Sub
End If
Application.Calculation = xlCalculationManual '自動計算オフ
Application.EnableEvents = False 'イベントオフ
lblTime.Caption = "" '所要時間クリア
Dim t As Long
t = GetTickCount '計測開始
Dim i As Long
Dim n As Long, M As Long
Dim x As Long, y As Long
Dim w() As Long
ReDim w(Nmax)
w(1) = 1
For n = 2 To Nmax
If w(n) = 0 Then
For i = 2 To Int(Nmax / n)
w(n * i) = 1
Next i
End If
Next n
With Sheets("ウラムの螺旋")
'作業枠幅設定
ColW = Application.WorksheetFunction.RoundUp(Sqr(Nmax), 0) '切り上げ
If (ColW Mod 2) = 0 Then ColW = ColW + 1 '偶数だったら直上の奇数に
'シート初期化
Call InitSheet_ウラムの螺旋(ColW)
'中心セル座標
x0 = Int(ColW / 2) + 1
y0 = Int(ColW / 2) + 1
.Cells(y0, x0).Select '選択
M = 1
n = 0
.Cells(y0, y0).Interior.Color = vbRed
For i = 1 To Nmax
If blCancel Then Exit For 'キャンセルボタンが押された
If (i Mod 1000) = 0 Or i = Nmax Then
lblProgress.Caption = i & "/" & Nmax '進行状況
lblTime.Caption = _
Format((GetTickCount - t) / 1000, "#,##0.00秒") '所要時間
DoEvents
End If
If w(i) = 0 Then
n = n + 1
GetSpiralPos i, x, y
.Cells(y + y0, x + x0) = i 'セルに数値表示
.Cells(y + y0, x + x0).Interior.Color = vbCyan
End If
Next i
End With
Application.Calculation = xlCalculationAutomatic '自動計算オン
Application.EnableEvents = True
End Sub
Private Function GetSpiralPos(n As Long, ByRef x As Long, ByRef y As Long)
'
' うずまき座標取得 出発点を(0,0)とする相対座標
'
Dim w As Long '一辺の長さ
Dim w2 As Long
Dim L As Long '中心から最大相対位置
Dim P As Long '完全平方からの不足数
Dim M As Long
'外接する正方形の幅
M = Application.WorksheetFunction.RoundUp((Sqr(n) + 1) / 2, 0)
'
' (2m-1)^2 ≦ n 奇数幅の正方形升目数 m:1,2,3・・・
'
w = 2 * M - 1 '正方形の幅
w2 = w - 1 '一辺幅-1
L = Int(w / 2)
P = w ^ 2 - n '完全平方からの不足数
Select Case P
Case Is < w2 * 1
x = L: y = L - P
Case Is < w2 * 2
x = L - (P Mod w2): y = -L
Case Is < w2 * 3
x = -L: y = (P Mod w2) - L
Case Is < w2 * 4
x = (P Mod w2) - L: y = L
End Select
End Function
フェルマーの小定理(Fermat's little theorem)
素数を使用した
合同
式の計算に、「
フェルマーの小定理」という強力な
ツール があります。
(「小」が付くのは、かの有名な「
フェ
ルマーの最終定理」と区別するため)
定理
p を素数とし、 a を p の倍数でない( a と p
は互いに素:a ≢ 0
(mod p))とすると
ap-1≡1(mod p)
である。
→ 分かりやすく書くと ・・・
p が素数で、かつ、a が p で割り切れないとすると、
a を p-1 乗したものを p で割った余りは 1
例: a=2、p=3 の場合
23-1≡22≡4≡1 (mod 3)
4≡1 (mod 3) は、4を3で割った余り(3をmod「modulas-法」と
する)と、
1を3で割った余りは合同(「≡」剰余だけを考えれば等しいグループ)であることを意味。
ここでは「フェルマーの小定理」の証明に、下記の補助定理を利用します。
補助定理
p を素数とし、a を a ≢ 0(mod p)
であるものとする。
この時、数列
a,2a,3a,・・・(p-1)a (mod p)
は、数列
1,2,3,,・・・(p-1) (mod p)
と順序を除いて一致する。
補助定理の証明
リスト a,2a,3a,・・・(p-1)a は
a と p は互いに素、および、1,2,3・・p-1 は p より小さいことから、pでは割り切れない。
このとき、このリストから2つの数 ja、ka をとり
ja ≡ ka (mod p)
が成り立つと仮定する。
この時、p|(j-k)a であり、pはaを割らないとした仮定より
p|(j-k) となる → (j-k)はpで割り切れる
ここで、1≦j、k≦(p-1) なので、|j-k|<(p-1) となる。
絶対値がpより小さく、pで割り切れる数は 0 しかない。
これは、j=kを意味する。
すなわち、リスト a,2a,3a,・・・(p-1)a にある数は全て異なる数である。
(証明終)
「フェルマーの定理」の証明
補助定理より
a,2a,3a,・・・(p-1)a (mod a) -① と
1,2,3,・・・(p-1) (mod a) -② は
順序を除いて同じものである。
よって、①の数列の積と②の数列の積は等しいので
a・(2a)・(3a)・・・((p-1)a)≡1・2・3・・・(p-1) (mod p)
これを書き直すと
ap-1(p-1)!≡(p-1)! (mod a)
(p-1)!とpは互いに素であるから、両辺から消すと
ap-1≡1 (mod p)
が得られる。 (証明終)
以下はa=3として、p=199までで計算してみた例
p=3ではpとaが互いに素でないために成立しませんが、その他は見事に成立しています。
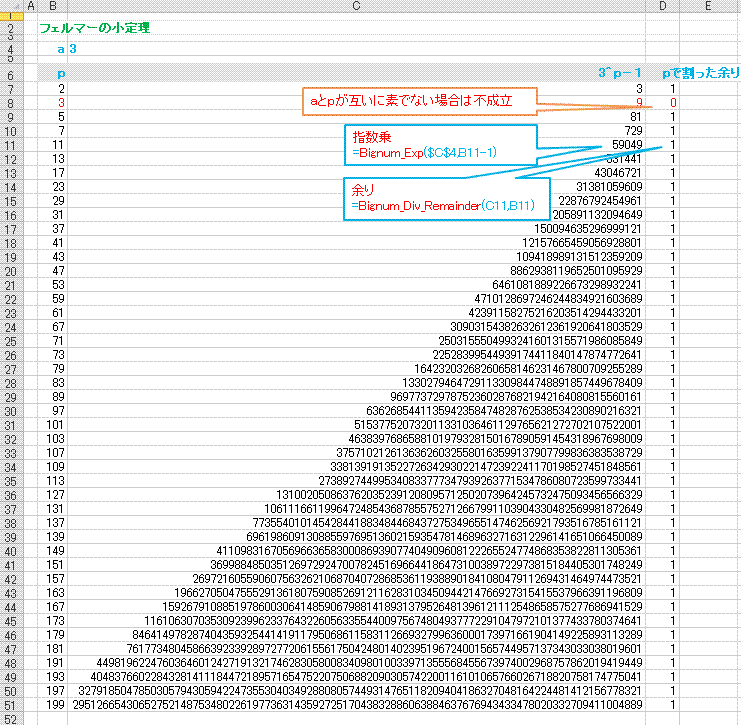
「フェルマーの小定理」の応用例
今日は日曜日。では、2の1000乗日後の曜日は?
曜日は7つなので、法を7とした余りを考えればよいことになります。
さて、2の1000乗を7で割った余りは?
7は素数なので「フェルマーの小定理」が使えそうです。
小定理は、2
6=2
7-1≡1 (mod 7)と言っています。
さて1000乗の場合は、
2
1000=2
6x166+4=(2
6)
166・2
4
(mod 7)
ここで、2
6≡1 (mod 7) なので
2
4 (mod 7) のみを計算すればよいことになります。
すなわち
16 ≡ 2 (mod 7)
よって、今日が日曜日であれば、2の1000乗日後の曜日は、今日から2日後の曜日と同じ。
すなわち、
火曜日ということになりますね。
普通、こんな問題は出ませんが、
このような方法は、
公開暗号作成などに頻繁に使用されています。
なお、「
フェルマーの小定理」を
拡張
したものが「
オイラーの定理 」となります。
リンクリスト