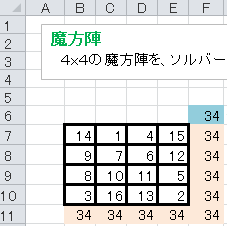
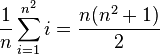正方形の方陣に数字を配置し、縦・横・斜めのいずれの列についても、
その
列の数字の合計が同じになるもののこと。
1辺がn個のマス目の場合、1列の和は
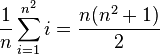
となります。
すなわち、3x3の場合は
15、
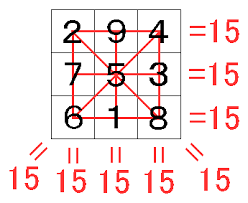
4x4の場合は
34。
合計の求め方
一辺がnである正方形の升目には、n×n 個の数字が入ります。
1からnまでの連続する整数の和は、n×(n+1)/2 、n x n までだと n2×(n2 +1)/2 となります。
ここで、n x n の正方形には n個の行 があります。
また、各行の和は等しい(魔方陣の定義)ので、それを S とすると、n×S は全体の和と等しくなるはずです。
よって、1行の和 Sは、 n×(n2 +1)/2 となります。 −以上
とりあえず1〜9までの数字を正方形に並べ、
その縦、横、右上がり斜め、左上がり斜めのそれぞれの合計を算出する式を設定します。

制約条件
・入力セルの数値は、非負の整数。
・同じく、すべて異なる1以上9以下の数値。
・縦横斜め、それそれの合計は15
ただし、このままでは、目標セルが無いので、合計のセル一つを、
目標のセルにします。
ここでは、セル
F6(薄水色のセル)
下図3番目の条件、「
AllDifferent」はエクセル2010から登場した新機能。
「
全て異なる」という制約条件になります。
これで、1〜9までの数値を1個ずつ割り当てられます。

以上でシミュレーションを行うと、ほとんど瞬間的に解が求まります。

同じようににて、
4x4の魔方陣を作成してみます。

条件式は、3x3と同じ、ただし、範囲が異なります。
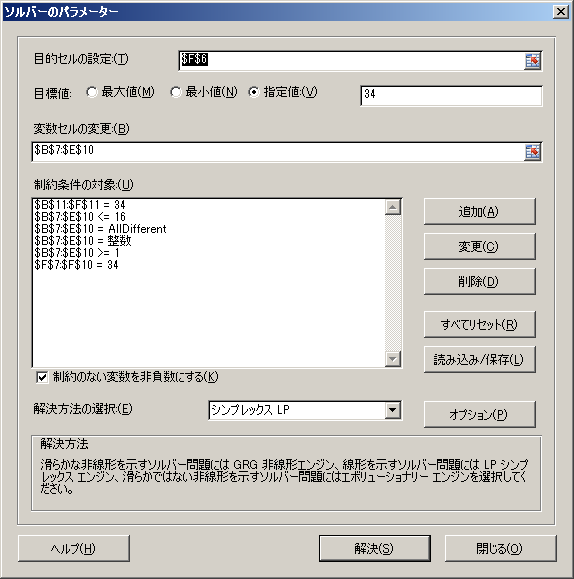
実行すると、今度は、かなり時間が掛かります。
計算量が(辺数の二乗)の
階乗に比例するため、辺の数が多くなると、爆発的に時間が掛かるようになります。
このままの方法では、5x5を試してみようとも思いませんにね。